|
Moving Averages - Part 1 Part 1 | Part 2 |
| Introduction |
Moving averages are one of the most popular and easy to use tools available to the technical analyst. They smooth a data series and make it easier to spot trends, something that is especially helpful in volatile markets. They also form the building blocks for many other technical indicators and overlays.

The two most popular types of moving averages are the Simple Moving Average (SMA) and the Exponential Moving Average (EMA). They are described in more detail below.
| Simple Moving Average (SMA) |
(Click
here to see a live example of a Simple Moving Average)
A simple moving average is formed by computing the average (mean) price of a security over a specified number of periods. While it is possible to create moving averages from the Open, the High, and the Low data points, most moving averages are created using the closing price. For example: a 5-day simple moving average is calculated by adding the closing prices for the last 5 days and dividing the total by 5.
The calculation is repeated for each price bar on the chart. The averages are then joined to form a smooth curving line - the moving average line. Continuing our example, if the next closing price in the average is 15, then this new period would be added and the oldest day, which is 10, would be dropped. The new 5-day simple moving average would be calculated as follows:
Over the last 2 days, the SMA moved from 12 to 13. As new days are added, the old days will be subtracted and the moving average will continue to move over time.
In the example above, using closing prices from Eastman Kodak (EK), day 10 is the first day possible to calculate a 10-day simple moving average. As the calculation continues, the newest day is added and the oldest day is subtracted. The 10-day SMA for day 11 is calculated by adding the prices of day 2 through day 11 and dividing by 10. The averaging process then moves on to the next day where the 10-day SMA for day 12 is calculated by adding the prices of day 3 through day 12 and dividing by 10.
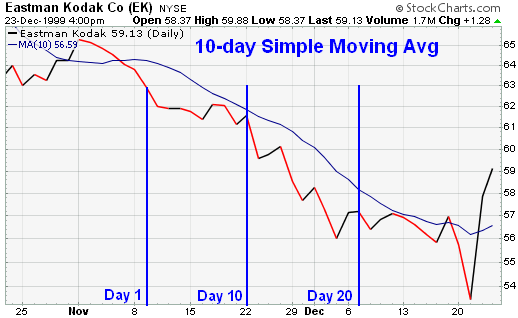
The chart above is a plot that contains the data sequence in the table. The simple moving average begins on day 10 and continues.
This simple illustration highlights the fact that all moving averages are lagging indicators and will always be "behind" the price. The price of EK is trending down, but the simple moving average, which is based on the previous 10 days of data, remains above the price. If the price were rising, the SMA would most likely be below. Because moving averages are lagging indicators, they fit in the category of trend following indicators. When prices are trending, moving averages work well. However, when prices are not trending, moving averages can give misleading signals.
| Exponential Moving Average (EMA) |
(Click
here to see a live example of an Exponential Moving Average)
In order to reduce the lag in simple moving averages, technicians often use exponential moving averages (also called exponentially weighted moving averages). EMAs reduce the lag by applying more weight to recent prices relative to older prices. The weighting applied to the most recent price depends on the specified period of the moving average. The shorter the EMA's period, the more weight that will be applied to the most recent price. For example: a 10-period exponential moving average weighs the most recent price 18.18% while a 20-period EMA weighs the most recent price 9.52%. As we'll see, the calculating and EMA is much harder than calculating an SMA. The important thing to remember is that the exponential moving average puts more weight on recent prices. As such, it will react quicker to recent price changes than a simple moving average. Here's the calculation formula.
Exponential Moving Average Calculation
Exponential Moving Averages can be specified in two ways - as a percent-based
EMA or as a period-based EMA. A percent-based EMA has a percentage as it's
single parameter while a period-based EMA has a parameter that represents the
duration of the EMA.
The formula for an exponential moving average is:
EMA(current) = ( (Price(current) - EMA(prev) ) x Multiplier) + EMA(prev)
For a percentage-based EMA, "Multiplier" is equal to the EMA's specified percentage.
For a period-based EMA, "Multiplier" is equal to 2 / (1 + N) where N is the specified number of periods.
For example, a 10-period EMA's Multiplier is calculated like this:
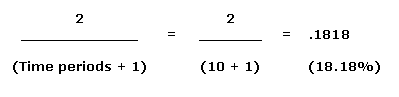
This means that a 10-period EMA is equivalent to an 18.18% EMA.
Note: StockCharts.com only support period-based EMAs.
Below is a table with the results of an exponential moving average calculation for Eastman Kodak. For the first period's exponential moving average, the simple moving average was used as the previous period's exponential moving average (yellow highlight for the 10th period). From period 11 onwards, the previous period's EMA was used. The calculation in period 11 breaks down as follows:

*The 10-period simple moving average is used for the first calculation only.
After that the previous period's EMA is used.
(Click
here to download this table as an Excel spreadsheet.)
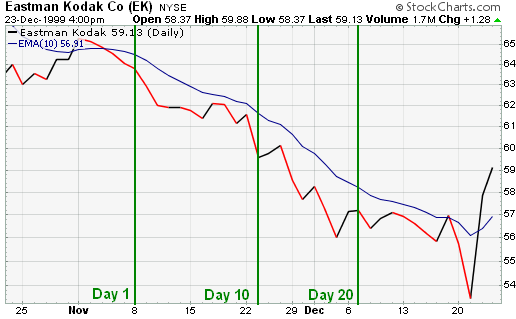
Note that, in theory, every previous closing price in the data set is used in the calculation of each EMA that makes up the EMA line. While the impact of older data points diminishes over time, it never fully disappears. This is true regardless of the EMA's specified period. The effects of older data diminish rapidly for shorter EMAs than for longer ones but, again, they never completely disappear.
| Simple Versus Exponential |
From afar, it would appear that the difference between an exponential moving average and a simple moving average is minimal. For this example, which uses only 20 trading days, the difference is minimal, but a difference nonetheless. The exponential moving average is consistently closer to the actual price. On average, the EMA is 3/8 of a point closer to the actual price than the SMA.


From day 10 to day 20, the EMA was closer to the price than the SMA 9 out of 10 times. The only time the SMA was closer was in period number 18, and this did not last long. The average absolute difference between the exponential moving average and the current price was 1 and the simple moving average had an average absolute difference of 1.33. This means that on average, the exponential moving average was 1 point above or below the current price and the simple moving average was 1.33 points above or below the current price.
When EK stopped falling and started to trade flat, the SMA kept on declining. During this period, the SMA was closer to the actual price than the EMA. The EMA began to level out with the actual price and remain further away. This was because the actual price started to level out. Because of its lag, the SMA continued to decline and even touched the actual price on 13-Dec.
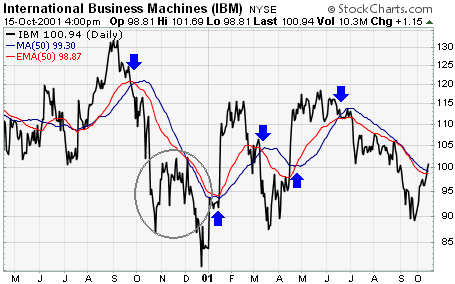
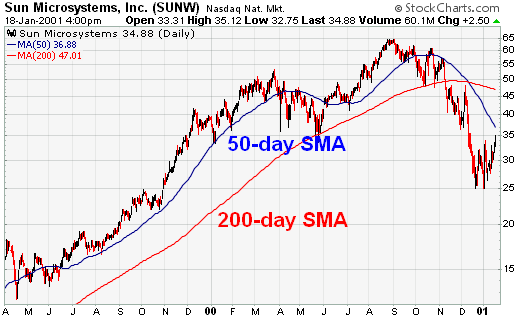
A comparison of a 50-day EMA and a 50-day SMA for IBM also shows that the EMA picks up on the trend quicker than the SMA. The blue arrows mark points when the stock started a strong trend. By giving more weight to recent prices, the EMA reacted quicker than the SMA and remained closer to the actual price. The gray circle shows when the trend began to slow and a trading range developed. When the change from trend to trading began, the SMA was closer to the price. As the trading range continued into 2001, both moving averages converged. In early 2001, CPQ started to trend up and the EMA was quicker to pick up on the recent price change and remain closer to the price.
| Which is better? |
Which moving average you use will depend on your trading and investing style and preferences. The simple moving average obviously has a lag, but the exponential moving average may be prone to quicker breaks. Some traders prefer to use exponential moving averages for shorter time periods to capture changes quicker. Some investors prefer simple moving averages over long time periods to identify long-term trend changes. In addition, much will depend on the individual security in question. A 50-day SMA might work great for identifying support levels in the Nasdaq, but a 100-day EMA may work better for the Dow Transports. Moving average type and length of time will depend greatly on the individual security and how it has reacted in the past.
The initial thought for some is that greater sensitivity and quicker signals are bound to be beneficial. This is not always true and brings up a great dilemma for the technical analyst: the trade off between sensitivity and reliability. The more sensitive an indicator is, the more signals that will be given. These signals may prove timely, but with increased sensitivity comes an increase in false signals. The less sensitive an indicator is, the fewer signals that will be given. However, less sensitivity leads to fewer and more reliable signals. Sometimes these signals can be late as well.
For moving averages, the same dilemma applies. Shorter moving averages will be more sensitive and generate more signals. The EMA, which is generally more sensitive than the SMA, will also be likely to generate more signals. However, there will also be an increase in the number of false signals and whipsaws. Longer moving averages will move slower and generate fewer signals. These signals will likely prove more reliable, but they also may come late. Each investor or trader should experiment with different moving average lengths and types to examine the trade-off between sensitivity and signal reliability.
In Part 2, we examine how to use moving averages to identify support and resistance levels, recognize trends and develop a trading system.
Part 1 | Part 2